SISTEMA DE ECUACIONES DE PRIMER Y SEGUNDO GRADO
Ecuaciones de primer y segundo grado
Una ecuación de primer grado es una igualdad que tiene una o más variables elevadas a la primera potencia, resolverlas significa encontrar el valor de las variables con los que se cumple la igualdad.
Ecuaciones de primer grado
- Con una incógnita
Hay unos pasos generales a seguir para resolver una ecuación de primer grado y son los siguientes:
1.- Reducir términos semejantes si es posible
2.- Pasar al lado izquierdo los términos con incógnitas y al lado derecho los que no tienen, esto se hace con las operaciones inversas, es decir si en un lado se está sumando, al otro lado de la igualdad se pasa restando.
3.- Despejar la incógnita.
Ejemplo
Tenemos la siguiente ecuación:
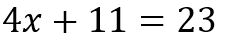
No hay términos semejantes así que pasamos a separar los términos con incógnita al lado izquierdo de la ecuación y los que no tienen los pasamos al lado derecho.
4x = 23 – 11
4x = 12
Ahora solo nos falta despejar la ecuación
x = 12/4
Como respuesta a la ecuación de primer grado obtenemos que el valor de la variable es 3.
- Con dos incógnitas
Las ecuaciones de primer grado con dos incógnitas tienen infinitas soluciones, pues el valor de una variable depende del valor que le des a la otra, es decir :
si tenemos la siguiente ecuación
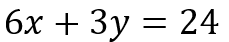
y despejamos la”x” obtenemos lo siguiente:
x = (24 – 3y)/6
O sea que dependiendo del valor que le demos a la “y” será el valor de “x”. Construimos una tabla:

Para obtener un valor exacto tendríamos que tener una segunda ecuación y resolverlas mediante los métodos para resolver sistemas de ecuaciones.
Ecuaciones de segundo grado
Empecemos primero por definir que es una ecuación de segundo grado… Una ecuación de segundo grado es aquella que tiene la forma ax² + bx + c, donde a, b, y c son números reales y a es diferente a cero, por ejemplo:
4x² + 3x + 12 = 0 a=4, b=3, c=12
6x² – 5x = 0 a=6, b=-5, c=0
Como resolver ecuaciones de segundo grado
Hay tres formas de resolver las ecuaciones de segundo grado y encontrar el valor de las variables:
1.- Factorización simple
2.- Completando el cuadrado
3.- Formula cuadrática
- Factorización simple
Como resolver ecuaciones de segundo grado por factorización?
Este método consiste en resolver la ecuación como un producto de binomios, es decir encontrar dos números que multiplicados den como resultado “c” y sumados den “b”.
Este método se usa cuando a = 1.
Ejemplo:
x² + 1x – 12 = 0
Encontramos que 4 · (-3) = -12 y 4 + (-3) = 1
(x + 4)(x – 3) = 0
x + 4 =0 despejando; x = -4
x – 3 = 0 despejando; x = 3
las dos soluciones son x = -4 y x = 3.
Completando el cuadrado
Como resolver ecuaciones de segundo grado por el método completando el cuadrado?
Para utilizar este método debemos adaptar nuestra ecuación a la forma ax²+bx+c y que “a” sea igual a 1.
Si en nuestra ecuación “a” fuera diferente a 1 tendríamos que dividir toda la ecuación entre “a”.
Para resolverla primero hacemos lo siguiente:
ax² + bx + ___ = c + ___
ax² + bx + (b/2)² = c + (b/2)²
y después factorizamos la ecuación (siempre será un cuadrado perfecto)
( ) ( ) = c + (b/2)²
Ejemplo:
2x² + 12x + 16 = 0 /2
x² + 6x + 8 = 0 (6/2)²=9
x² + 6x + 9 = -8 + 9
x² + 6x + 9 = 1
(x + 3)(x + 3) = 1
(x + 3)² = 1
x + 3 = ± 1
x = -3 ± 1
las soluciones son x = -4, x = -2
- Formula cuadrática
Simplemente sustituimos nuestros valores de a, b y c en la formula y obtendremos los valores de x.
Ejemplo:
x² + 7x + 12 = 0
x = (-7 ± (49 -48 )1/2)/2
x = (-7 ± 1)/2
x = (-7 + 1)/2 = -4
x = (-7 – 1)/2 = -3
Las soluciones son x = -4, x = -3
Ya que has aprendido qué son las ecuaciones de primer y segundo grado y sabes cómo resolverlas, solamente te falta practicar con algunos ejercicios de ecuaciones de primer y segundo grado.
https://matematicasmodernas.com/ecuaciones-de-primer-y-segundo-grado/
https://matematicasmodernas.com/ecuaciones-de-primer-y-segundo-grado/
No hay comentarios.:
Publicar un comentario