Un sistema de m ecuaciones lineales con n incógnitas (SEL) y coeficientes en un cuerpo K (como los reales o los complejos) es:

donde

A los elementos ai , j se les denomina coeficientes del SEL y a los bi términos independientes.
Un ejemplo de un SEL de dos ecuaciones y dos incógnitas es:

El sistema de la definición lo podemos expresar matricialmente como:

donde

Veamos un ejemplo:

https://www.matesfacil.com/matrices/matrices-sistemas.html
SISTEMAS DE ECUACIONES LINEALES POR ELIMINACIÓN:
Básicamente consiste en hacer nulos los elementos que hay debajo de los aii con i= 1, 2, 3, ..., m-1 ; y el rango final será el número de filas distintas de cero.
* En una etapa i cualquiera se deja fija la fila i , y tomando como referencia el elemento aii por medio de operaciones elementales se hacen cero todos los elementos de su columna (los que estén por debajo de él).
* Si el elemento aii es igual a cero, es preciso intercambiar previamente esa fila por alguna otra fila de debajo, y si no es posible (porque también sea cero) con alguna columna de la derecha, hasta conseguir que aii sea distinto de cero (es conveniente, para evitar cálculos tediosos que sea 1, si no lo fuera, utilizando operaciones sencillas intentaremos cambiarlo a 1).
Finalmente, el rango es el número de filas distintas de cero que aparecen en la matriz.
Ejemplo:
Hallar el rango de la matriz
Hacemos 0 los elementos debajo de a11: Sustituimos F2 por F2 - 3F1, similarmente F3 por F3 - 2F1 ,...
El rango de ambas matrices será el mismo:
Ahora intercambiamos la fila F2 con la F4 (sigue siempre siendo el mismo rango):
Ahora hacemos 0 los elementos debajo del a22: sustituimos F3 por F3 - 7F2:
Y ya tenemos ceros por debajo de la diagonal. El rangode A es 3 (cantidad de filas no nulas).
http://www.ehu.eus/juancarlos.gorostizaga/mateI15/T_matrdeter/MatrDeter
Método de reducción:
Se preparan las dos ecuaciones para que una de las incógnitas tenga el mismo coeficiente en ambas. Al restarlas o sumarlas se obtiene una ecuación sin esa incógnita.
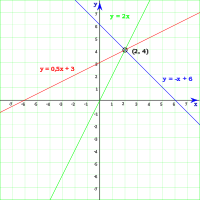
Método gráfico:
Consiste en construir la gráfica de cada una de las ecuaciones del sistema. El método (manualmente aplicado) solo resulta eficiente en el plano cartesiano, es decir para un espacio de dimensión.
El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resuelve en los siguientes pasos:
Se despeja la incógnita en ambas ecuaciones.
Se construye para cada una de las dos ecuaciones de primer grado obteniendo la tabla de valores correspondientes.
Se representan gráficamente ambas rectas en los ejes coordenados.
SISTEMAS SINGULARES:
Los valores singulares son objetos muy ´utiles en Algebra Lineasl Num´erica y han ´
recibido mucha atenci´on durante los ´ultimos a˜nos. El objetivo es introducirlos a una
audiencia general de manera elemental aprovechando su interpretaci´on geom´etrica.
Se presentar´an tambi´en algunas aplicaciones mostrando su inter´es en dos
campos: en el an´alisis num´erico y en el tratamiento de im´agenes. Debido a su fuerte
naturaleza geom´etrica, en la presentaci´on oral se utiliz´o un GUI (Graphical User Interface)
de MATLAB2 del que se expondr´an aqu´ı algunas im´agenes que, esperamos,
sirvan para facilitar la compresi´on de los conceptos.
No hay comentarios.:
Publicar un comentario